Building Autoencoders in Keras
원문: Building Autoencoders in Keras
이 문서에서는 autoencoder에 대한 일반적인 질문에 답하고, 아래 모델에 해당하는 코드를 다룹니다.
주요 키워드
- a simple autoencoders based on a fully-connected layer
- a sparse autoencoder
- a deep fully-connected autoencoder
- a deep convolutional autoencoder
- an image denoising model
- a sequence-to-sequence autoencoder
- a variational autoencoder
Note: 모든 예제 코드는 2017년 3월 14일에 Keras 2.0 API에 업데이트 되었습니다. 예제 코드를 실행하기 위해서는 Keras 버전 2.0 이상이 필요합니다.
autoencoder는 무엇일까요?
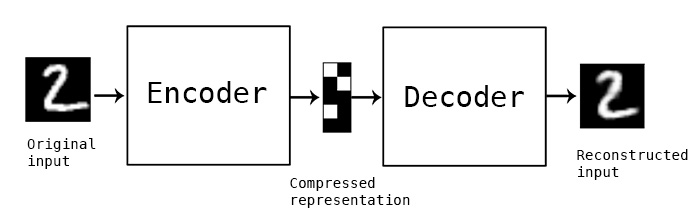
“Autoencoding” 은 데이터 압축 알고리즘으로 압축 함수와 압축해제 함수는 다음과 같은 세가지 특징을 갖습니다: 1) data-specific, 2) 손실(lossy), 3) 사람의 개입 없이 예제를 통한 자동 학습. 추가적으로 “autoencoder” 가 사용되는 대부분의 상황에서 압축 함수와 압축해제 함수는 신경망으로 구현되는 경향이 있습니다. 각 특징에 대해 자세히 알아보겠습니다.
- autoencoder는 data-specific 합니다. autoencoder는 이제껏 훈련된 데이터와 비슷한 데이터로만 압축될 수 있습니다. 예를 들어 말하자면, autoencoder는 MPEG-2 Audio Layer III (MP3) 압축 알고리즘과는 다릅니다. MP3 알고리즘은 일반적으로 소리에 관한 압축이지만 특정한 종류의 소리에 관한 것은 아닙니다. 얼굴 사진에 대해 학습된 autoencoder는 나무의 사진을 압축하는 데에는 좋은 성능을 내지 못하는데 그 이유는 autoencoder가 배우는 특징은 얼굴 특유의 것이기 때문입니다.
- autoencoder는 손실이 있습니다. 즉, 압축 해제된 결과물은 원본 보다 좋지 않습니다 (ex. MP3, JPEG 압축). 이는 손실없는 산술 압축과는 다릅니다.
- autoencoder는 예제 데이터로부터 자동적으로 학습하는데 이는 유용한 성질입니다: 데이터로부터 자동적으로 학습한다는 의미는 특정 종류의 입력값에 대해 잘 작동하는 특별한 형태의 알고리즘을 쉽게 훈련시킬 수 있다는 말입니다. 이는 새로운 공학적 방법 필요 없이 단지 데이터를 적절히 훈련시키면 됩니다.
autoencoder를 만들기 위해서는 세 가지가 필요합니다.
- 인코딩 함수 (encoding function)
- 디코딩 함수 (decoding function)
- 원본에 대해 압축된 표현(representation)과 압축 해제된 표현(representation) 간 정보 손실량 간의 거리 함수 (즉, 손실 함수)
인코더와 디코더는 parametic 함수(일반적으로 신경망) 로 선택되고 거리 함수와 관련하여 차별화되므로 인코딩/디코딩 함수의 매개변수를 확률적 경사하강법(Stochastic gradient descent)을 사용하여 재구성 손실을 최소화하도록 최적화 할 수 있습니다.
간단합니다! 이러한 단어를 모른다고 걱정하지 마세요. 이 실습 예제는 이런 단어를 몰라도 시작할 수 있습니다.
autoencoder는 데이터 압축에 좋을까요?
일반적으로는 그렇지 않습니다.
사진 압축에서 JPEG와 같은 기본 알고리즘보다 나은 성능을 내는 autoencoder를 개발하는 것은 꽤 어렵습니다. 일반적으로 JPEG의 성능에 도달할 수 있는 유일한 방법은 사진을 매우 특정한 유형으로 제한하는 것입니다. autoencoder가 data-specific 하다는 점 때문에 autoencoder는 실제 데이터 압축 문제에 적용하기에 비실용적입니다. 따라서 autoencoder는 훈련된 것과 비슷한 데이터에서만 사용될 수 있고, autoencoder를 일반적인 데이터에 대해 사용하기 위해서는 많은 훈련 데이터가 필요합니다. 하지만 미래에는 바뀔 수도 있습니다, 모르는 일이지요.
autoencoder는 어디에 쓰일까요?
autoencoder는 실제 응용에서는 거의 사용되지 않습니다.
2012년, autoencoder를 응용할 수 있는 방법이 deep convolutional neural network에 대한 greedy layer-wise pretraining 에서 발견되었습니다 [1]. 그러나 random weight initialization schemes가 처음부터 deep network를 훈련하기에 충분하다는 것을 알게되면서 autoencoder는 빠르게 유행에서 사라졌습니다. 2014년, batch normalization[2]은 훨씬 더 깊은 network를 허용하기 시작했고, 2015년 말부터 residual learning을 사용하여 임의적으로 deep network를 훈련시킬 수 있었습니다[3].
오늘날 autoencoder의 두 가지 흥미로운 실제 응용분야는 data denosing과 데이터 시각화를 위한 차원 축소입니다. 적절한 dimensionality와 sparsity contraints를 사용하면, autoencoder는 PCA나 다른 기법들보다 더 흥미로운 data projection을 배울 수 있습니다.
특히 2차원 시각화에 대하여, t-SNE는 거의 최고의 알고리즘입니다. 하지만 이는 상대적으로 낮은 차원의 데이터를 요구합니다. 따라서 높은 차원의 데이터에서 유사(similarity) 관계를 시각화하는 좋은 전략은 먼저 autoencoder를 사용하여 데이터를 낮은 차원으로 압축하는 것입니다. 그리고나서 압축된 데이터를 t-SNE를 사용하여 2차원 평면으로 매핑합니다. 이미 케라스의 휼륭한 parametric implementation를 Kyle McDonald가 개발하였고, github에서 볼 수 있습니다. 또한, scikit-learn에도 간단하고 실용적으로 구현되어 있습니다.
그렇다면 autoencoder는 왜 중요할까요?
autoencoder가 유명해진 주된 이유는 온라인의 수많은 머신러닝 수업에 특집으로 등장하기 때문입니다. 이렇다보니, 머신러닝 분야의 많은 입문자는 autoencoder를 매우 좋아합니다. 이것이 이 튜토리얼이 존재하는 이유죠!
autoencoder가 수많은 연구와 집중을 끌어들이는 또다른 이유는 autoencoder가 비지도 학습(unsupervised learning)의 문제를 풀어낼 잠재적인 수단으로 오랜동안 생각되었기 때문입니다. 다시 한번 말하자면, autoencoder는 진정한 비지도 학습(unsupervised learning) 기술이 아니라, self-supervised 기술입니다. 이는 지도 학습(supervised learning)의 일종으로 입력 데이터로부터 타겟을 만들어냅니다. 흥미로운 특징(feature)들을 학습하는 self-supervised model을 얻으려면 흥미로운 합성 목표 및 손실 함수를 제공해야 합니다. 문제는 여기서 발생합니다.
단순히 빠르게 입력값을 재구성 하는 것을 학습시키는 것은 여기서 그렇게 좋은 선택이 아닙니다. 예를 들어, 픽셀 수준에서 사진의 재구성에 초점을 맞추는 것은 label-supervised learning에서 얻을 수 있는 흥미롭고 추상적인 특징 ‘(feature)’을 배우는데 도움이 되지 않는다는 중요한 증거가 있습니다 (타겟이 ‘개’나 ‘자동차’처럼 인간이 발명해낸’’ 추상적인 개념들인 경우). 사실, 이와 관련된 가장 좋은 특징(feature)은 다음과 같습니다. 정확하게 입력 재구성이 힘든 동시에, 범주화나 지역화 같은 여러분이 관심있는 주요 작업에서 높은 성능을 달성하는 것입니다.
비전(vision)에 적용되는 self-supervised learning에서, autoencoder 스타일의 입력 재구성에 대한 잠재적으로 유용한 대안은 다음과 같습니다. 직소 퍼즐 해결 또는 세부 컨텍스트(context) 매칭(고해상도이지만 그림의 작은 조각들을 그 조각들이 추출된 그림의 저해상도 버전으로의 매칭을 가능하게 함)같은 작은 작업을 사용하는 것입니다.
다음 논문은 직소 퍼즐 문제를 조사하여 흥미로운 결과를 냈습니다: Noroozi and Favaro(2016) Unsupervised Learning of Visual Representation by Solving Jigsa Puzzles. 이러한 작업은 “픽셀 수준의 세부 정보를 넘어서는 시각적 매크로 구조 문제“와 같은 기존의 autoencoder 에는 없는 입력 데이터에 대한 가정을 제공합니다.

매우 간단한 autoencoder를 만들어봅시다.
간단한 것에서 시작합시다. 인코더와 디코더로 single fully-connected neural layer를 사용합니다.
from keras.layers import Input, Dense
from keras.models import Model
# 인코딩될 표현(representation)의 크기
encoding_dim = 32 # 32 floats -> 24.5의 압축으로 입력이 784 float라고 가정
# 입력 플레이스홀더
input_img = Input(shape=(784,))
# "encoded"는 입력의 인코딩된 표현
encoded = Dense(encdoing_dim, activation='relu')(input_img)
# "decoded"는 입력의 손실있는 재구성 (lossy reconstruction)
decoded = Dense(784, activation='sigmoid')(encoded)
# 입력을 입력의 재구성으로 매핑할 모델
autoencoder = Model(input_img, decoded)
분리된 인코더 모델도 만듭시다.
# 이 모델은 입력을 입력의 인코딩된 입력의 표현으로 매핑
encoder = Model(input_img, encoded)
디코더 모델도 만듭니다.
# 인코딩된 입력을 위한 플레이스 홀더
encoded_input = Input(shape=(encoding_dim,))
# 오토인코더 모델의 마지막 레이어 얻기
decoder_layer = autoencoder.layers[-1]
# 디코더 모델 생성
decoder = Model(encoded_input, decoder_layer(encoded_input))
이제 우리의 autoencoder로 MNIST 숫자를 재구성해봅시다.
먼저, 픽셀 당 바이너리 크로스엔트로피 손실을 사용하도록 모델을 구성하고, optimizer로 Adadelta를 사용합시다.
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
입력 데이터를 준비합시다. MNIST 숫자를 사용할 것이고, 라벨은 버리도록 하겠습니다. 입력 이미지를 인코딩하고 디코딩하는 데에만 관심이 있기 때문이죠.
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
모든 값을 0~1 사이로 정규화하고 28x28 이미지를 크기 784의 벡터로 만들겠습니다.
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
print x_train.shape
print x_test.shape
이제 autoencoder를 50 epoch 동안 훈련시키죠.
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
50 epoch 이후, autoencoder는 약 0.11의 안정적인 train/test 손실 값에 도달하였습니다. 재구성된 입력과 인코딩된 표현(representation)을 시각화 해봅시다. Matplotlib을 이용하겠습니다.
# 숫자들을 인코딩 / 디코딩
# test set에서 숫자들을 가져왔다는 것을 유의
encoded_imgs = encoder.predict(x_test)
decoded_imgs = decoder.predict(encoded_imgs)
# Matplotlib 사용
import matplotlib.pyplot as plt
n = 10 # 몇 개의 숫자를 나타낼 것인지
plt.figure(figsize=(20, 4))
for i in range(n):
# 원본 데이터
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# 재구성된 데이터
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
아래에 결과가 있습니다. 위의 줄은 원래의 숫자이고 아랫 줄은 재구성된 숫자입니다. 지금 사용한 간단한 접근 방법으로 꽤 많은 비트 손실이 있었다는 것을 알 수 있습니다.

Adding a sparsity constraint on the encoded representations
이전 예제에서, 표현(representation)은 은닉층의 크기(32)에만 제약을 받았습니다. 이러한 상황에서, 전형적으로 발생하는 일은 은닉층이 PCA(principal component analysis)의 근사값을 학습한다는 것입니다. 표현을 더 간결하게 제한하는 다른 방법은 숨겨진 표현의 활동에 sparsity를 부여하는 것입니다. 이는 주어진 시간에 더 적은 유닛이 “실행”될 수 있도록 합니다. Keras에서는 activity_regularizer를 Dense layer에 추가하여 수행할 수 있습니다.
from keras import regularizers
encoding_dim = 32
input_img = Input(shape=(784,))
# L1 activity regularizer를 Dense layer에 추가
encoded = Dense(encoding_dim, activation='relu',
activity_regularizer=regularizers.l1(10e-5))(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input_img, decoded)
우리 모델을 100 epoch 동안 훈련시킵시다. 모델은 0.11의 train loss와 0.10의 test loss로 끝납니다. 이 둘의 차이가 발생하는 이유는 대부분 훈련 중 손실에 추가되는 정규화때문입니다.
새로운 결과를 보시죠.
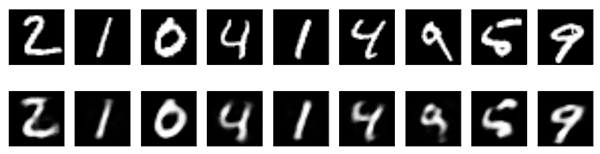
이전 모델과 거의 비슷해보입니다. 유일한 차이라면 인코딩된 표현의 sparsity입니다. encoded_imgs.mean()은 10,000개의 테스트 이미지에서 3.33의 값을 얻었지만, 이전 모델에서는 7.30이었습니다. 따라서, 우리의 모델은 두 배 더 sparser한 인코딩 된 표현을 만들어냈습니다.
Deep autoencoder
이제 더이상 인코더나 디코더 같은 단일 layer에 제한을 가질 필요가 없습니다. 이제 다음과 같은 layer의 스택을 사용합시다.
input_img = Input(shape=(784,))
encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoded = Dense(32, activation='relu')(encoded)
decoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='sigmoid')(decoded)
다음과 같이 시도해보세요:
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
epochs=100,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
100 epoch 이후, train/test loss는 ~0.097까지 도달합니다. 이전 모델보다 조금 더 나아졌죠. 재구성된 숫자 또한 더 나아보입니다.
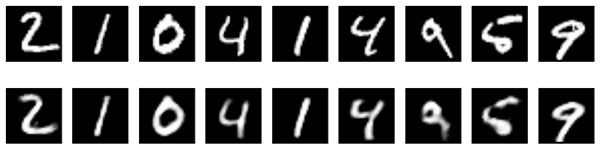
Convolutional autoencoder
우리가 사용하는 입력은 이미지이기 때문에, convolutional neural networks(convnet)을 인코더/디코더로 사용하는 것이 가능합니다. 실제로, 이미지에 적용되는 autoencoder는 항상 convolutional autoencoder입니다. 왜냐하면 성능이 더 좋기 때문이죠.
한 번 구현해 봅시다. 인코더는 Conv2D와 MaxPooling2D layer의 층으로 구성되고, 디코더는 Conv2D와 UpSampling2D layer의 층으로 구성됩니다.
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K
input_img = Input(shape=(28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
x = Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)
# 이 시점에서 표현(representatoin)은 (4,4,8) 즉, 128 차원
x = Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(16, (3, 3), activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
훈련을 위해서, 원본 MNIST 숫자의 shape (samples, 3, 28, 28)을 사용하고, 픽셀 값만 0~1로 정규화하도록 하겠습니다.
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
50 epoch 동안 훈련시키죠. 모델 훈련 과정을 시각화하여 설명하기 위해, Tensorflow 백엔드와 TensworBoard 콜백을 사용할 것입니다.
먼저, 터미널을 열고 /tmp/autoencoder에 저장된 로그를 읽는 서버인 TensorBoard를 시작합시다.
tensorboard --logdir=/tmp/autoencoder
이제 모델을 훈련시킵시다. callback 리스트에서 TensorBoard callboack 인스턴스를 전달합니다. 매 epoch 이후, 이 콜백은 TensorBoard 서버에서 읽을 수 있는 /tmp/autoencoder에 로그를 씁니다.
from keras.callbacks import TensorBoard
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=128,
shuffle=True,
validation_data=(x_test, x_test),
callbacks=[TensorBoard(log_dir='/tmp/autoencoder')])
TensorBoard 웹 인터페이스(http://0.0.0.0:6006)에서 훈련 과정을 모니터링할 수 있습니다.
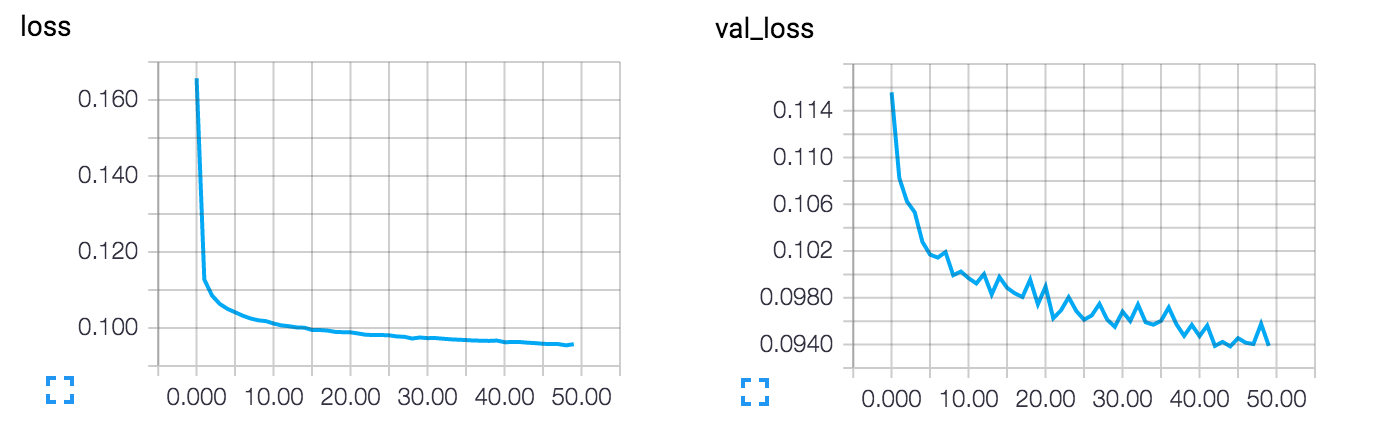
이 모델은 0.094의 손실 값으로 수렴합니다. 이는 명백히 이전 모델보다 나아졌지요(this is in large part due to the higher entropic capacity of the encoded representation, 128 dimensions vs. 32 previously). 재구성된 숫자를 한 번 봅시다.
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# 원본 출력
ax = plt.subplot(2, n, i)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# 재구성본 출력
ax = plt.subplot(2, n, i + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
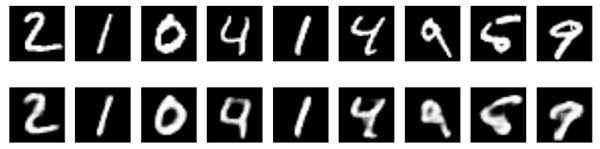
또한, 128차원의 인코딩된 표현으로도 볼 수 있습니다. 이 표현은 8x4x4이기 때문에 그레이스케일 이미지에서 나타내기 위해 4x32로 reshape해야합니다.
n = 10
plt.figure(figsize=(20, 8))
for i in range(n):
ax = plt.subplot(1, n, i)
plt.imshow(encoded_imgs[i].reshape(4, 4 * 8).T)
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

이미지 denosing 응용
이제 우리의 convoultional autoencoder를 이미지 denoising 문제에 적용해봅시다. 매우 간단합니다: 노이지(noisy)한 숫자 이미지를 클린(clean)한 숫자 이미지로 매핑하는 autoencoder를 훈련시키면 됩니다.
아래는 합성 노이즈가 있는 숫자를 생성하는 방법입니다. 가우스 노이즈 행렬을 적용하여 이미지를 0과 1사이에서 잘라내면 됩니다.
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
노이즈가 있는 숫자는 다음과 같습니다.
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

자세히 들여다보면 어떤 숫자인지 알 수 있지만 알아보기 힘듭니다. 어떻게 autoencoder는 원본 숫자로 복원하는 법을 배울 수 있었을까요? 알아봅시다.
이전의 convolutional autoencoder와 비교해서, 재구성된 이미지의 질을 향상시키려면, 약간 다른 모델을 사용하여 layer 당 더 많은 필터를 사용합니다.
input_img = Input(shape=(28, 28, 1)) # 'channels_firtst'이미지 데이터 형식을 사용하는 경우 이를 적용
x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)
# 이 시점에서 표현(representation)은 (7,7,32)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
100 epoch 동안 훈련시켜보죠.
autoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test),
callbacks=[TensorBoard(log_dir='/tmp/tb', histogram_freq=0, write_graph=False)])
이제 결과를 봅시다. 위는 네트워크에게 준 노이즈가 있는 숫자입니다. 그리고 밑의 이미지는 네트워크가 재구성한 숫자들이죠.

만족할만한 결과입니다. 이 과정을 더 큰 convnet으로 확장하고 싶다면, 문서 denoising이나 오디오 denoising 모델 구축을 시작할 수 있습니다. Kaggle이 당신의 시작을 위한 데이터셋을 가지고 있어요!
Sequence-to-sequence autoencoder
벡터나 2D 이미지가 아닌 입력값이 연속적이라면, 인코더와 디코더를 시간 구조를 잡을 수 있는 모델을 사용하고 싶을 것입니다. LSTM같은 것 말이죠. LSTM 기반의 autoencoder를 만들기 위해서는, 먼저 LSTM 인코더를 사용하여 입력 시퀀스를 전체 시퀀스에 대한 정보가 들어있는 단일 벡터로 변환하고, 그 벡터를 n번 반복합니다 (n은 출력 시퀀스의 timestep의 수입니다). 그리고 이 일정한 시퀀스를 타겟 시퀀스로 바꾸기 위해 LSTM 디코더를 실행합니다.
여기서 데이터에 대해 설명하지는 않겠습니다. 이는 독자의 미래 관심사에 대한 예제 코드일 뿐이니까요.
from keras.layers import Input, LSTM, RepeatVector
from keras.models import Model
inputs = Input(shape=(timesteps, input_dim))
encoded = LSTM(latent_dim)(inputs)
decoded = RepeatVector(timesteps)(encoded)
decoded = LSTM(input_dim, return_sequences=True)(decoded)
sequence_autoencoder = Model(inputs, decoded)
encoder = Model(inputs, encoded)
Variational autoencoder(VAE)
Variational autoencoder은 약간 더 현대적이면서 흥미로운 autoencoding 입니다.
Variational autoencoder가 뭘까요? 이는 학습된 인코딩 표현에 대한 제약 조건이 추가된 autoencoder 입니다. 더 정확히 말하자면, 입력 데이터에 대한 latent variable model 을 학습하는 autoencoder라고 할 수 있습니다. 따라서, 신경망에게 임의의 함수를 학습시키는 대신, 데이터를 모델링하는 확률 분포의 매개 변수를 학습시킵니다. 만약, 이 분포에서 점(points)를 샘플링하면, 새로운 입력 데이터의 샘플 또한 생성할 수 있습니다: VAE는 “생성 모델” 입니다.
어떻게 variational autoencoder가 작동하는 걸까요?
먼저, encoder 네트워크는 입력 샘플 x를 잠재공간(latent space)에서 두 개의 매개 변수로 변환합니다. 이 매개 변수는 z_mean과 z_log_sigma를 나타냅니다. 그런 다음, z = z_mean + exp(z_log_sigma) * epsilon 을 통해 데이터를 생성한다고 가정한 잠재정규분포(latent normal distribution)에서 유사한 점 z를 무작위로 샘플링합니다. 여기서, epsilon은 임의의 정규텐서(normal tensor)입니다. 마지막으로, decoder 네트워크는 이러한 잠재 공간의 점을 원래의 입력 데이터로 다시 매핑합니다.
모델의 매개 변수는 두 가지 손실 함수를 통해 훈련됩니다: 디코딩된 샘플을 초기 입력과 일치하도록하는 재구성 손실 (이전의 autoencoder 처럼), 그리고 regularzation term처럼 작동하는 잠재 분포(latent distribution)과 사전 분포(prior distribution) 간의 KL 발산. 후자는 잘 형성된 잠재 공간(latent space)을 학습하고 훈련 데이터의 과적합(overfitting)을 줄이는 데 도움이 되지만, 후자를 완전히 삭제하도록 하겠습니다.
VAE는 복잡한 예시이기 때문에, Github에 코드를 공개 해놓았습니다. 여기서는 어떻게 모델이 단계별로 생성되는지만 보겠습니다.
먼저, 잠재 분포 매개변수와 입력을 매핑하는 encoder 네트워크입니다.
x = Input(batch_shape=(batch_size, original_dim))
h = Dense(intermediate_dim, activation='relu')(x)
z_mean = Dense(latent_dim)(h)
z_log_sigma = Dense(latent_dim)(h)
이 매개변수를 사용하여 잠재 공간에서 새로운 유사점을 샘플링할 수 있습니다.
def sampling(args):
z_mean, z_log_sigma = args
epsilon = K.random_normal(shape=(batch_size, latent_dim),
mean=0., std=epsilon_std)
return z_mean + K.exp(z_log_sigma) * epsilon
# Tensorflow 백엔드에서는 "output_shape"가 필요하지 않습니다.
# 따라서, `Lambda(sampling)([z_mean, z_log_sigma])` 라고 쓸 수 있습니다.
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_sigma])
결과적으로, 이러한 샘플링된 잠재 점(point)을 재구성된 입력으로 다시 매핑할 수 있습니다.
decoder_h = Dense(intermediate_dim, activation='relu')
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
x_decoded_mean = decoder_mean(h_decoded)
지금까지 우리가 한 것은 3가지 모델을 구체화한 것입니다.
- 입력과 재구성(reconstruction)을 매핑하는 end-to-end autoencoder
- 입력과 잠재공간(latent space)을 매핑하는 encoder
- 잠재 공간(latent space)에서 점을 샘플링할 수 있고, 이에 대응 되는 재구성된 샘플을 출력할 수 있는 generator
# end-to-end autoencoder
vae = Model(x, x_decoded_mean)
# encoder, 입력과 잠재공간을 매핑
encoder = Model(x, z_mean)
# generator, 잠재공간과 재구성된 입력을 매핑
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
generator = Model(decoder_input, _x_decoded_mean)
재구성 term과 KL 수렴 정규 term의 합을 손실 함수로 가지는 end-to-end 모델을 사용하여 모델을 학습시킵니다
def vae_loss(x, x_decoded_mean):
xent_loss = objectives.binary_crossentropy(x, x_decoded_mean)
kl_loss = - 0.5 * K.mean(1 + z_log_sigma - K.square(z_mean) - K.exp(z_log_sigma), axis=-1)
return xent_loss + kl_loss
vae.compile(optimizer='rmsprop', loss=vae_loss)
MNIST 숫자에 대해 VAE를 학습시킵니다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
vae.fit(x_train, x_train,
shuffle=True,
epochs=epochs,
batch_size=batch_size,
validation_data=(x_test, x_test))
우리의 잠재 공간(latent space)가 2차원이기 때문에, 이 시점에서 할 수 있는 좋은 시각화가 있습니다. 그 중 하나는 잠재 2D 평면에서 다른 범주를 가진 이웃을 보는 것입니다.
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()
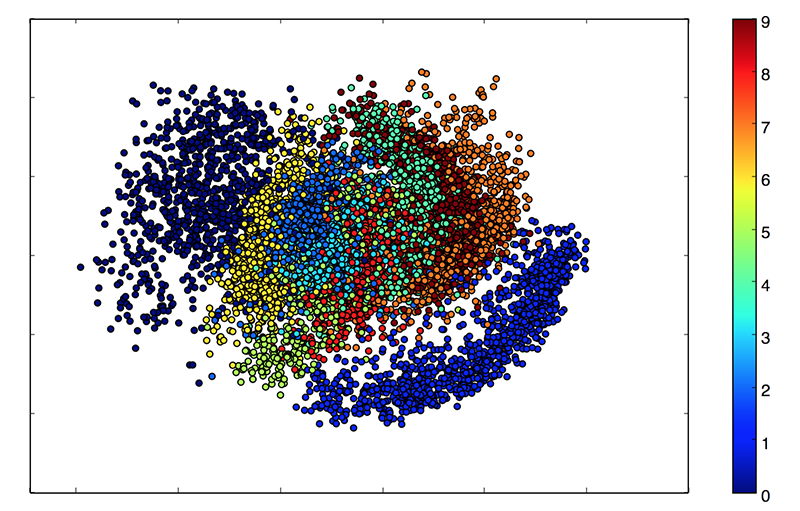
이러한 색깔의 클러스터는 숫자의 종류입니다. 가까운 클러스터는 구조적으로 비슷한 숫자입니다(즉, 잠재 공간에서 정보를 공유하는 숫자).
VAE가 생성 모델이기 때문에, 우리는 새로운 숫자도 만들어낼 수 있습니다! 여기서는 잠재 평면을 스캔하고 일정한 간격으로 잠재 지점(point)를 샘플링 한 다음, 점 각각에 해당하는 숫자를 생성해내겠습니다. 이는 MNIST 숫자를 “생성”하는 잠재 매니폴드(manifold)의 시각화를 제공합니다.
# 숫자의 2D manifold 출력
n = 15 # 15x15
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# we will sample n points within [-15, 15] standard deviations
grid_x = np.linspace(-15, 15, n)
grid_y = np.linspace(-15, 15, n)
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]]) * epsilon_std
x_decoded = generator.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.show()

끝입니다! 이 게시물(또는 이후의 게시물)에서 다루어졌으면 좋겠는 주제가 있다면, 트위터 @fchollet를 통해 연락 주세요.
References
[1]Why does unsupervised pre-training help deep learning?
[2]Batch normalization: Accelerating deep network training by reducing internal covariate shift.
[3]Deep Residual Learning for Image Recognition
[4]Auto-Encoding Variational Bayes
이 글은 2018 컨트리뷰톤에서 Contribute to Keras 프로젝트로 진행했습니다.
Translator : 윤정인
Translator email : [asdff2002@gmail.com] (asdff2002@gmail.com)